共分散構造分析
共分散構造分析とは
- 共分散構造分析は「多変量解析」の分析手法のひとつであり、ある事象に対する因果関係の仮説を検証する分析手法です。
- 解析によって得られる結果から、因果関係の向きと強さが明らかになります。
- 例えば、「商品やブランドのリピート率を高めるには、ロイヤリティの向上が重要である」という仮説を立てたとして、 その仮説が正しいのか、正しいとすればどの程度の強い因果関係があるのか、を解明します。
- また、その仮説を元にロイヤリティの向上を目指すとすれば、どのような要因との因果関係が強いのかも明らかにできるので、 マーケティングミックス(戦略)への落とし込みが可能になります。
マーケティングリサーチの解析において、「相関関係がある」、「因果関係がある」といった言葉をよく耳にされると思います。
どちらも同じことのように思われますが、相関関係と因果関係は異なります。因果関係があれば必ず相関関係があります。
ただし、相関関係があるからといって、必ずしも因果関係が存在するとは限りません。
相関関係の強さを示す指標に相関係数がよく用いられますが、因果関係の強さと混同すると、
データから得られた結果を読み誤ることになります。
共分散構造分析は、複数の変数間の仮説的な因果関係を検証し、その因果関係の強さを明らかにする「多変量解析」と
呼ばれる分析手法のひとつです。多変量解析は、目的変数(外的基準)と説明変数(内的基準)の因果関係を明らかにする手法と、
質問項目や回答した対象者の整理、分類、類似度を明らかにする手法に大別され、前者を「目的変数(外的基準)のある手法」、
後者を「目的変数(外的基準)をもたない手法」と言います。共分散構造分析は、後者の「目的変数(外的基準)のある手法」であり、
多くの変数間の因果関係の仮説的な構造を検証し、因果関係の強さを明らかにする手法です。
代表的な多変量解析の手法は、解析するデータによって以下のように分類されます。
【代表的な多変量解析の手法】
| 目的変数(外的基準)の種類 | 説明変数(内的基準)の種類 | 解析手法 | |
|---|---|---|---|
| 目的変数(外的基準)がある | 数量 | 数量 | 重回帰分析 |
| 数量 | 分類(カテゴリー) | 数量化理論Ⅰ類 | |
| 分類(カテゴリー) | 数量 | 判別分析 | |
| 分類(カテゴリー) | 分類(カテゴリー) | 数量化理論Ⅱ類 | |
| 一対比較/順位(得点・ランク) | 分類(カテゴリー) | コンジョイント分析 | |
| 数量 | 数量 | 共分散構造分析(SEM) | |
| 目的変数(外的基準)がない | - | 数量 | 因子分析 |
| - | 数量 | 主成分分析 | |
| - | 数量/クロス集計表 | コレスポンデンス分析 | |
| - | 数量 | 数量化理論Ⅳ類 | |
| - | 数量 | クラスター分析 | |
| - | 分類(カテゴリー) | 数量化理論Ⅲ類 |
共分散構造分析は、分析者が変数間の因果関係について仮説を立てるところから始めます。
仮説は変数項目間を矢印で結んだ「パス図」と呼ばれる図で表します。共分散構造分析を行うことで、
変数項目間の関係性の強さを表す「パス係数」と呼ばれる値が算出され、パス図の矢印上に示されます。
ちなみに「共分散構造分析」という名称は「Covariance Structure Analysis」を訳したもので、
共分散や分散を想起させますが、この分析手法の本論ではないので「構造方程式モデリング」と呼ばれることもあります。
そのため、英語表記である「Structural Equation Modeling」の頭文字から「SEM」とも呼ばれますが同じ分析手法です。
また、仮説的なパス図を描く上での決め事があります。アンケート調査や観測によって得られたデータを「観測変数」といい、
パス図では四角に囲んで表現します。また、アンケート調査や観測では得られなかったが、仮説的に存在するであろうと思う変数項目を
「潜在変数」と言い、パス図では楕円で囲んで表現します。因果関係において原因に当たる変数を「原因項目」、
結果に当たる変数を「結果項目」とし、それぞれを矢印の始点と終点で結びます。原因項目同士の因果関係を表す場合、
その項目間の時間的な意味を勘案して時間的に前にある項目を始点とします。
共分散構造分析事例
ある商品のユーザーのロイヤリティの構造とリピート率との関係性を明らかにするために共分散構造分析を行います。 まず、構造的な仮説として以下のようなパス図を作成しました。
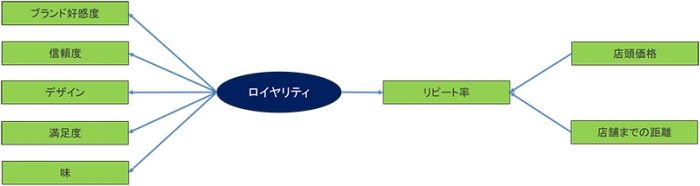
ここで、潜在変数である「ロイヤリティ」以外は、アンケート調査や顧客の販売データからの観測変数が存在するので、 その数値を用いて共分散構造分析を実行します。「ロイヤリティ」は「ブランド好感度」「信頼度」「デザイン」「満足度」 「味」に対する評価を因子分析した結果から求められます。さらに「リピート率」と「ロイヤリティ」「店頭価格」 「店舗までの距離」の関係は重回帰分析によって分析がなされます。解析の結果、以下のようなパス係数が算出されました。
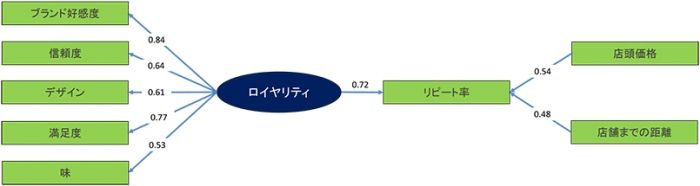
パス係数は相関係数とは違い値が1を超えることもあるので、いくつに近づけば関係性が強いという基準はありません。
得られた値がパス図の中で大きい項目ほど因果関係が強いと言えます。
分析の適合度については以下のような「適合度指標」と「検定値」によって判断されます。
①適合度指標
GFI(Goodness-of-Fit Index)
重回帰分析における「決定係数」に相当します。最大値は1であり、1に近づくほど分析がうまくいったと判断します。
一般的な目安は「0.9以上」です。
RMSEA(Root Mean Square Error of Approximation)
最小値は0であり、0に近づくほど分析がうまくいったと判断されます。一般的な目安は「0.05以下」です。
RMR(Root Mean square Residual)
最小値は0であり、0に近づくほど分析がうまくいったと判断されます。
②検定値
カイ二乗検定のp値を適用します。有意水準0.05よりも大きければ「パス図は真実である」と判断されます。
逆に、優位水準0.05を下回る場合は「パス図は真実でない」と仮説は棄却されます。
今回の解析ではすべての適合度の基準を満たしており、分析はうまくいったと判断しました。
この解析結果から、以下のようなことが読み取れます。
1:「リピート率」に対する影響度は、「ロイヤリティ」「店頭価格」「店舗までの距離」の中では「ロイヤリティ」が最も強い。
2:「ロイヤリティ」への影響度は、「ブランド好感度」が最も強く、「満足度」「信頼度」がそれに続く。
3:総合すると、売上拡大のために「リピート率」を向上させるには、価格政策や店舗政策よりも「ロイヤリティ」を
向上させることが重要であり、「ロイヤリティ」の向上には「ブランド好感度」「満足度」「信頼度」の向上がカギとなる。
共分散構造分析 応用事例
共分散構造分析では、解明したい仮説からパス図を作成することが重要となります。 仮説は無限の可能性がありますので、それに対応したパス図も数限りなく描くことができます。 数多くの可能性の中から代表的なパス図で共分散構造分析の応用事例を見てみます。
①成分モデル
観測変数を始点、潜在変数を終点にしたパス図に共分散構造分析を実行すると、 主成分分析とほぼ同様の結果が得られます。以下は、4つの観測変数から1つの潜在変数を作成するモデルです。

②子分析モデル
潜在変数を始点、観測変数を終点にしたパス図に共分散構造分析を行うと、因子分析とほぼ同様の結果が得られます。

③2次因子分析モデル
4つの観測変数から2つの潜在変数を導き、さらに2つの潜在変数から1つの潜在変数を導出します。

④パス解析モデル
観測変数間の意識の時系列を勘案してパス図を作成し、共分散構造分析を適用するモデルです。

⑤重回帰モデル
複数の観測変数と1つの観測変数との因果関係を解析する場合のパス図となります。

⑥MIMICモデル(Multiple Indicator Multiple Cause)
4つの観測変数から主成分分析により1つの潜在変数(ブランド総合評価)を導出し、購入意向度との回帰分析を行うモデルです。

⑦PLSモデル(Partial Least Squares)
ここではブランド評価の4つの観測変数から主成分分析により潜在変数(総合満足度)を導出し、 リピート意向と推奨意向の2つの観測変数に因子分析を用いて潜在変数(購入意向度)を導きます。 2つの潜在変数(総合満足度と購入意向度)で回帰分析を行います。