重回帰分析
重回帰分析とは
「多変量解析」は要因と結果の因果関係を明らかにし、結果を予測する解析手法と、情報の整理、分類、類似度を明らかにする解析手法に大きく分かれます。「重回帰分析」は前者の予測する解析手法の一つです。
複数の要因とそれによって変動する結果の因果関係を明らかにし、そこからそれぞれの要因が結果に与えている影響度を算出し、結果を予測することが可能です。例えば企業や店舗の売り上げ、顧客満足度の評価向上には、どのような要因が重要な影響を与えているかなどの分析が可能です。企業の取引先別の取引額、営業訪問回数、販売担当の満足度、値引率などの営業データから、それぞれの要因の重要度を探ることもできます。
予測結果の精度が高ければ、予測モデル式として要因の目標値や変動値をモデル式に当てはめ、将来の結果の変動を予測するシミュレーションをすることも可能になります。また、目標の取引額を達成するためには、営業訪問回数、販売担当の満足度、値引率などの要因をどれくらい向上させれば目標額を達成できるかという逆シミュレーションを行うことも可能です。
代表的な多変量解析の手法は、解析するデータによって以下のように分類されます。
【代表的な多変量解析の手法】
| 目的変数(外的基準)の種類 | 説明変数(内的基準)の種類 | 解析手法 | |
|---|---|---|---|
| 目的変数(外的基準)がある | 数量 | 数量 | 重回帰分析 |
| 数量 | 分類(カテゴリー) | 数量化理論Ⅰ類 | |
| 分類(カテゴリー) | 数量 | 判別分析 | |
| 分類(カテゴリー) | 分類(カテゴリー) | 数量化理論Ⅱ類 | |
| 一対比較/順位(得点・ランク) | 分類(カテゴリー) | コンジョイント分析 | |
| 数量 | 数量 | 共分散構造分析(SEM) | |
| 目的変数(外的基準)がない | - | 数量 | 因子分析 |
| - | 数量 | 主成分分析 | |
| - | 数量/クロス集計表 | コレスポンデンス分析 | |
| - | 数量 | 数量化理論Ⅳ類 | |
| - | 数量 | クラスター分析 | |
| - | 分類(カテゴリー) | 数量化理論Ⅲ類 |
重回帰分析の特長
「 多変量解析」では原因となるデータを説明変数、結果となるデータを目的変数と呼びます。重回帰分析の特徴として、以下の3点が挙げられます。
- 数値で確認できる統計的な予測、推論の根拠となるデータ分析ができる。
- 複数の変数を用いるため、実用的な分析ができる。
- それぞれの変数の係数から、結果への影響度が判断できる。
重回帰分析は、説明変数の数が増えるほどデータ量だけでなく考察事項も増えるため、分析は複雑なものとなりがちです。数値で統計的な予測が立てられるので、ビジネスシーンでは主にプレゼンテーション資料などの根拠を示す説明やデータ分析に利用されています。
重回帰分析の手順
1 目的変数と説明変数を抽出する
目的変数と説明変数を抽出する目的変数と、相関関係のある複数の説明変数をデータから抽出します。例えば取引先別の取引額を目的変数、営業訪問回数、販売担当の満足度、値引き率を説明変数とするなどです。
2 モデル式を仮定する
取引額をY、X1を営業訪問回数、X2を販売担当の満足度、X3を展示会参加回数、X4を値引き率とした場合、
Y=aX1+bX2+cX3+dX4-eなど、異なる変数の関わりを示すモデル式が算出できます。
a、b、c、d、eには一定の数字が入ります。
3 集めた変数データを元に分析
モデル式が適正であるかを検証するために、実際の営業訪問回数、販売担当の満足度、値引き率の説明変数をモデル式に代入します。
重回帰分析事例
ある企業様の取引先別の営業データから重回帰分析により、次期売上の予測及び要因の重要度を探ってみたいと思います。
①次期売上予測
データセットの諸元は目的変数として「取引額」、説明変数には「営業訪問回数」「営業マン満足度」「展示会参加回数」「値引率」の4つが相関関係にあると判断しました。
・データ単位/内容
「取引額」:万円/年間
「営業訪問回数」:回/月
「営業マン満足度」:得点/5点満点(非常に不満1点~非常に満足5点)
「展示会参加回数」:回/年(四半期ごと年4回の展示会への参加回数)
「値引率」:%
取引先10社のデータをまとめると以下のようになっています。
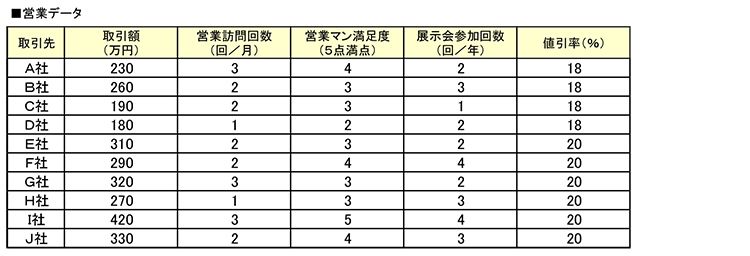
このデータから重回帰分析を行うと、以下のようなモデル式が得られました。
Y=37.9776x₁+3.9326x₂+23.0037x₃+38.1742x₄-605.955
Y:取引額、x₁:営業訪問回数、x₂:営業マン満足度、x₃:展示会参加回数、x₄:値引率、「-605.955」は定数項となります。
これで、今回の分析対象とした営業データのモデル式が導出された訳ですが、この式は果たして適正なモデル式となっているのでしょうか。検証してみるためには、上記のモデル式に実際の営業データの4つの説明変数を代入して取引額を算出した「理論値」と実際の取引額の「実績値」との乖離がどの程度あるのかを判断基準とします。この乖離の判定には、まずA社~J社までの「理論値」と「実績値」の相関係数を求めます。算出された相関係数は「重相関係数(R)」と言います。さらに重相関係数を2乗したものを「決定係数(R²)」と言い、重回帰分析では、この決定係数を分析精度の判定に用います。決定係数は0から1の値を取り、1に近いほど分析精度は高いと言えます。今回のデータの解析結果の決定係数は0.8721となっており、十分に精度の高いモデル式と言えます。
ここから、実際にモデル式を使って売上のシミュレーションを行ってみましょう。現在、10社の取引額を合計した売上額は2,800万円です。次期の営業活動は展示会に力を入れて取引先の担当者の参加回数をアップさせて売上拡大につなげたいと思った時のシミュレーションとして、年4回の展示会にすべての担当者に参加してもらったらと仮定して理論値を算出してみます。ただし、F社とI社の担当者は今期も4回参加しているので実績値のままと想定します。
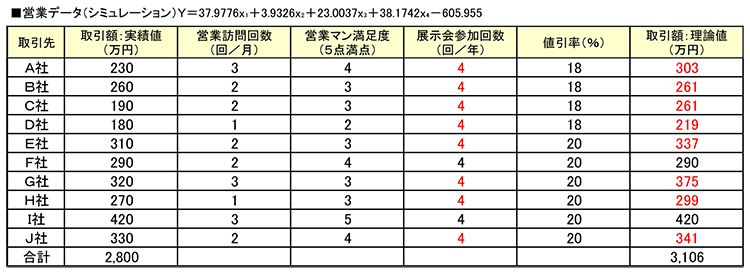
シミュレーションの結果をみると、この施策が実現できれば売上額は3,106万円となり、今期より306万円ほど拡大する可能性が見込まれます。
②要因の重要度
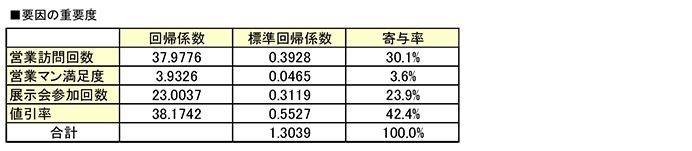
重回帰分析で導出された先ほどのモデル式のx₁からx₄に掛け合わされる数値は「回帰係数」と呼ばれ、取引額Yに対する貢献度を意味し、単位はYに等しく「万円」です。
説明変数(要因)の重要度はこの回帰係数の大きさとイコールではありません。なぜなら説明変数ごとの単位はもともとYや他の変数と違っているからです。この単位の違いを取り払った上で、重回帰分析を行い得られた回帰係数が重要度を判定する基準となります。この回帰係数を「標準回帰係数」と言います。
単位の違いを取り払うためには、各変数の「基準値」を求める必要があります。基準値は「(実測値-実測値の平均)÷標準偏差」で求められます。
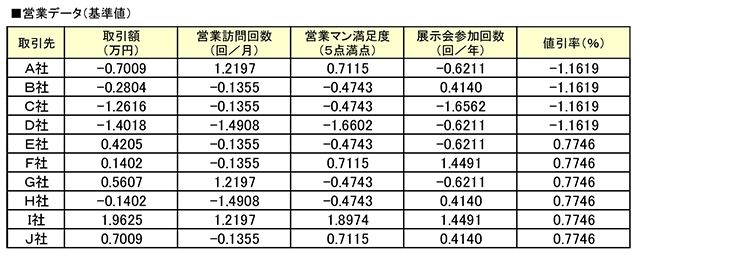
基準値を元に重回帰分析を行った結果、以下のような式が得られました。基準値による重回帰分析では定数項は0になります。
Y=0.3928x₁+0.0465x₂+0.3119x₃+0.5527x₄
これにより得られた標準回帰係数から説明変数(要因)間の相対的な重要度を判定します。通常は、標準回帰係数の合計を100%とした場合の各変数の占める割合の大きさで重要度は示されます。この各変数の標準回帰係数が占める割合を「寄与率」と呼びます。
標準値による重回帰でも「値引率」が最も重要度が高く、「営業マンの満足度」の重要度は最も低く、売上拡大には価格政策が重要なカギとなるようです。
重回帰分析 応用事例
重回帰分析のモデル式を応用して、以下のような分析も可能です。
・取引額を目標額として固定して、それを達成するためには各変数(要因)をどの程度向上させれば目標額を達成できるかを逆シミュレーションできます。例えば、売上目標○○万円、顧客満足度○○点を達成するための「行動成果目標」を理論的な数値目標で設定できます。