アンケート調査で得られたデータの集計方法の一つにクロス集計があります。今回は、クロス集計のメリットとクロス集計でできる分析について解説します。
クロス集計とは
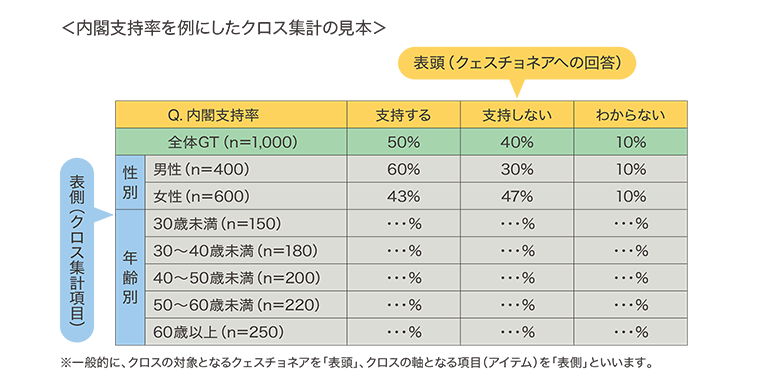
アンケートの結果をパーセントのような数値へ置き換えたものが集計です。例えば、選挙調査で「内閣を支持しますか？」という設問に対して、「支持する」50%、「支持しない」40%、「わからない」10%というように、〇〇%という割合に置き換えることが集計です。集計は、単純集計とクロス集計の大きく2つに分けられます。単純集計は、GT（グランドトータル）とも呼ばれ、アンケートの回答者数全体の実数や比率のことで、集計の基本となります。内閣支持率の例で示しますと、回収数（n）（*1）が1,000だとすれば、500（n）が支持、400（n）が不支持、100（n）が「わからない」ということになります。これを比率で表すと、支持50%、不支持40%、「わからない」10%となるわけです。これが単純集計です。
しかし、単純集計だけでは、全体の支持率はわかっても、どのような属性の人が内閣を支持しているのかまではわかりません。支持率を「性別で知りたい」、「年齢別で知りたい」、「選挙区別で知りたい」などの属性で知りたい場合が必ずと言ってよいほど発生します。
この属性別（基本属性＝デモグラフィック）のような層別で集計する方法がクロス集計です。当然、基本属性だけがクロス集計ではなく、買物調査の場合は来店頻度別、CS調査の場合は満足度別、広告効果測定調査の場合はテレビ視聴時間別など、調査の種類・目的によってさまざまな軸でクロス集計は活用されています。つまり、クロス集計をすることによって、GTの中身の詳細を知ることが可能になります。
クロス集計のメリット
クロス集計は、アンケート分析の基本です。例えば、性別、年代別での特徴や傾向などを分析するうえで、なくてはならないものです。性別×年代別を軸にした三重クロス集計も頻繁に活用されています。性別×年代別を分析軸にすることで、男性20代と女性20代の比較ができ、差異も明確に分かるようになるのです。しかし、このようなデモグラフィックを軸にした分析以外に、集計表として可視化することで新たな分析軸を発見することや表頭同士を組み合わせて分析軸を作成することも分析者として必要な能力となってきます。昨今は、エクセルなどの表計算ソフトのアドイン集計ソフトで、手軽にクロスする項目を選定して短時間で集計結果を得られ、分析者の仮説を簡単に検証できるようになりました。また、クロス集計分析は、多変量解析を行う場合のベースにもなりますので、マーケテイングリサーチャーとしては、GT分析と同様に基礎技術といえます。
クロス集計を基にできる分析
「クロス集計とは」「クロス集計のメリット」で既述しているようにクロス集計は、GTの中身を詳細に分析する、ということです。 その種類は以下のように大きく3つに分けられます。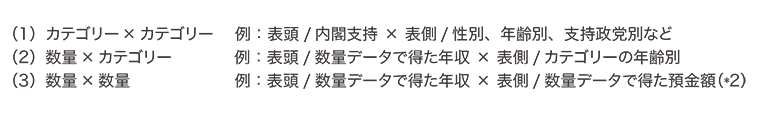
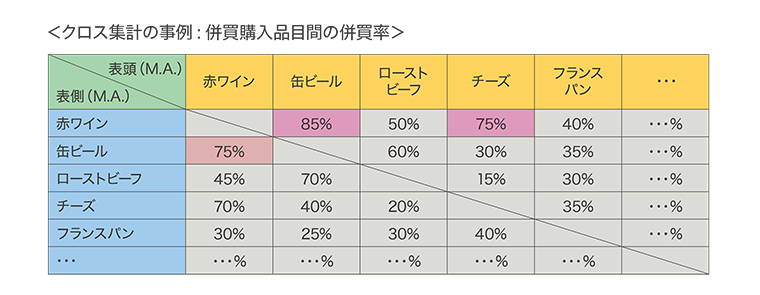
この集計表にある数値（%）は、併買率を示します。赤ワイン購入者の85%は缶ビールを、75%はチーズを購入しているということで、併買率は高いといえるでしょう。この比率を分析する限りにおいては、缶ビールの赤ワイン併買率も75%と高いので、アルコール類は同時に購入される比率が高いということが分かります。また赤ワインの場合、チーズの併買率も高いことから、チーズをワインの近くに置く、といったような陳列戦略も立てられます。
注意しておきたいクロス集計のデメリット
クロス集計は、非常に有効な分析手法であることは間違いないのですが、当然デメットもあります。まず、サンプリング調査の場合、分析に入る際にサンプル数（n）の制約を受けます。例えば、「性別×年齢別で細かく分析したい」と考えていても、女性20代といったような1つのカテゴリーのnが少なく、代表性を失ってしまうことが多々あります。統計学に基づけば、1カテゴリーのnが最低30は必要です。したがって、調査のサンプルサイズを決める際に重要なことは、どこまで詳細に分析するか、ということをあらかじめ決めておくことです。しかし、クロス集計分析の精度を高めれば高めるほど、サンプルサイズが大きく、コスト増となり、日程も長くなりがちです。サンプルサイズ、コスト、日程において妥協点を見極めて調査を実施するべきでしょう。
次は、1カテゴリーのnについてです。既述したことですが、昨今は集計ソフト、表計算ソフトでクロス集計が簡単に出来るようになりました。しかし、クロス集計した場合、確実に1カテゴリーのnは少なくなります。つまり、標本誤差が大きくなるということを意味しますので、有意差検定の知識を身につけておかなければなりません。事前にクロス集計結果に検定結果を表示させるという仕組みを取り入れることも視野に入れておくべきことの1つだと考えられますが、nによって、どれくらいの標本誤差があるのか、常に意識しておく必要があります。
また、クロス集計をペーパーで打ち出した場合、本のように分厚く、膨大な量になることが頻発します。分析者がクロス集計の結果を読み込み、解釈する時間は一向に短縮できていない、ということが現状だと想像されます。解決策としては、目的志向（最終的に何を明らかにすべきなのか、何を解決したいのか、など）でクロス集計項目を決定し、極力集計量を減らすことです。そうすることで、集計データ分析・解釈の効率化につながります。
■クロス集計に関するサービスの詳細はこちら
・データ集計・変換
・無料集計ツール「Cross Finder2」
*1
統計学では、 母集団の大きさを表す場合は、N（ラージエヌ）、その母集団からアンケートで得たサンプル数を表す場合は、n（スモールエヌ）を使用します。内閣支持率の例で説明すると、調査地域が東京都の有権者であれば、N＝東京都の有権者数、n＝回収数1,000ということになります。ちなみに、nは、Number of casesの略です。
*2
（3）の例については、分析する前にある程度の予想が立てられます。「貯金が多ければ、年収も高いであろう」という相関関係を予測しても妥当だと考えられます。しかし、最終的には相関係数を求めて、相関関係があるのか否かを実証する必要があります。
*3
数値はダミーです。
