クロス・マーケティングで実施した調査レポートを無料で提供しております。 ダウンロードしたい無料調査レポートの「Download」にチェックをつけて、「ダウンロードに進む」をクリックしてください。 カテゴリやタグから調査のテーマや内容別に検索することも可能です。
- その他
非階層クラスター分析 k-umeyama(2023年8月日本行動計量学会第51回大会特別セッション発表)
2023 / 09 / 28

非階層型クラスタリングの圧倒的な精度向上を達成する、独自手法「k-umeyama」を開発しました。「k-umeyama」の採用により、マーケティングや広告業界にとどまらず、クラスタリングが日常的に活用されている、画像処理やAIを用いた判断処理等、多くの分野で革新的な精度向上が実現可能となりました。
*「k-umeyama」は開発者である弊社梅山貴彦の名をとったものです
既にアカウントをお持ちの方
新規登録(無料会員登録)の方
無料会員のサービス内容
- 市場調査レポートを無料でダウンロードいただけます。
- 会員限定のセミナーに無料でご参加いただけます。
- 分析ツール「Cross Finder2」を無料でご利用いただけます。
登録は無料。メールアドレス等の簡単な入力のみ。1分で完了します。
1.68 MB (自動取得)
- 高い分類精度と再現性を持つ、革新的な非階層型クラスタリングを開発
- 因子分析や主成分分析がなくても、様々な単位のデータでクラスター分析が実行可能
「k-umeyama」の概要
k-umeyamaは、分析対象のすべてのデータを格納して分析をおこなうため、情報量が多くても、もれなく分析を実施することができます。データに対して、相関性を排除する因子分析や主成分分析などのデータ加工を介さず、全てのデータ同士の関係性を加味して、無理なく分類できます。また、データが類似しており違いが小さい場合、どのクラスターに分類されるかがこれまで不安定であったものを、シグモイド関数を利用して、データ間の距離の重み付けをより明確にすることにより、データ分類の精度を向上させることを可能にしました。
標準的な非階層型クラスタリングの抱える課題
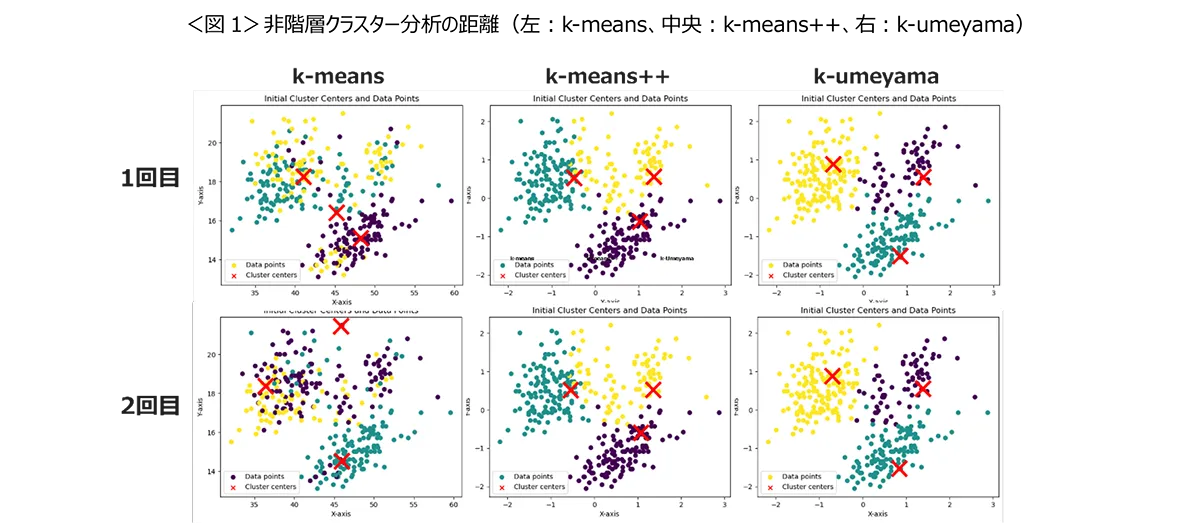
k-meansのアルゴリズムは、初期シードの選び方に依存して結果が変わり、そのシードが近くに偏ると、クラスタリングの質が低下する可能性が指摘されています。また、ランダムな選択方法により、再現性が低いという課題があります。下記の左側がk-meansのグラフとなりますが、初期シードが1回目と2回目では違う場所が指定され安定性が低いことがわかります。
これらの問題点を解決するための新しいアプローチとして、k-means++が開発されました。この方法では、初期シードを順番に選び出し、前のシードから距離が遠い次のシードを確率的に選択することで、クラスターが均等に分布するように配置されます。この改良により、クラスタリングの質と再現性が向上しました。中央がk-means++、右側がk-umeyamaとなり、それぞれシードの位置は違いますが。1回目と2回目のシードの位置は安定しています。しかし、k-means++は、シードの選択過程で、最も遠い点の外れ値が選ばれやすくなるという弱点があります。<図1>
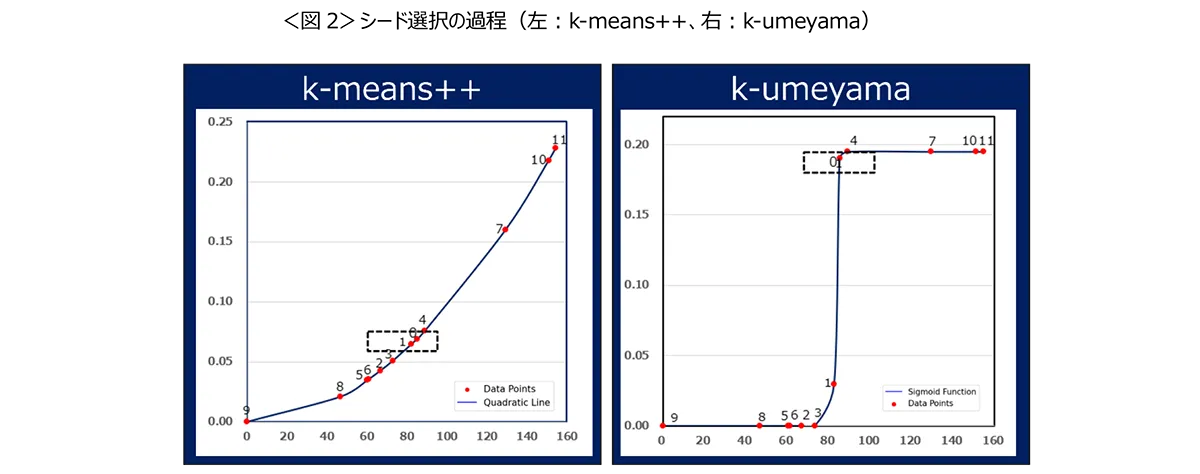
シードの選択過程の弱点改良に向けて、シグモイド関数を活用
弊社では、k-means++のシード選択に関する課題を解決すべく、新しい手法「k-umeyama」を開発いたしました。この方法は、シグモイド関数を活用することで、各データポイントが距離とウエイト値に基づいて明確に分類される特長があります。具体的な例として、グラフの左側をk-means++、右側をk-umeyamaとして表示した際、k-umeyamaによりデータポイント1や0を比較すると、ウエイトがk-means++(1=0.065,0=0.069)、k-umeyama(1=0.03,0=0.195)とはっきりとした分類となることが確認できます。この技術により、k-means++のシード選択の精度を一層向上させることが期待されます。<図2>
従来の非階層クラスター分析と距離の弱点改良に向けて
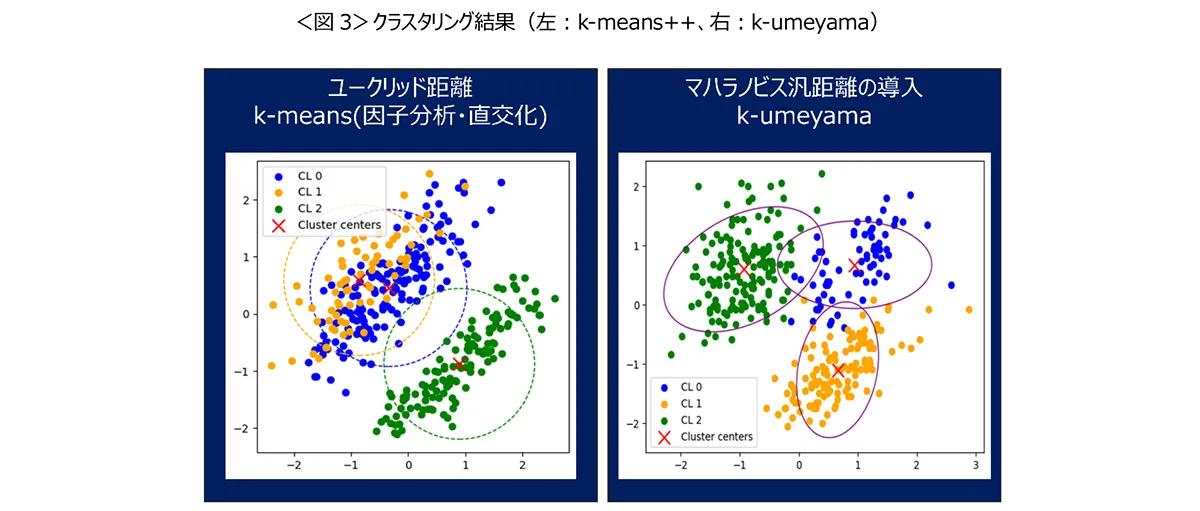
クラスター分析は、似た特徴を持つもの同士をグループにまとめる手法で、特にマーケティング・リサーチの業界でよく用いられます。一般的な手法、k-meansでは、最初にデータを「因子分析・直交化」という方法で整理します。これは、いろいろな情報を簡潔に表すためのステップですが、実は弱点があります。因子分析・直交化はデータの中の関連性を取り除く手法ですが、すべての集団が完璧に相関性を取り除いて整理されているわけではありません。また、因子分析・直交化をおこなうと、データ全体を表現する量が減少することもあります。グラフを用いて、因子分析・直交化したk-meansとマハラノビス汎距離を導入したk-umeyamaのクラスター分析の結果を比較したところ、その差異は一目瞭然となりました。グラフの左側は、因子分析による直交化を施したデータをk-meansでクラスタリングした結果です。こちらは、クラスター0と1が近接し、重なり合う正円の形をしていて、異なる集団がうまく分けられていないことを意味します。一方で、右側のグラフはマハラノビス汎距離を採用したk-umeyamaのクラスタリング結果です。こちらは、3つのクラスターが楕円の形状をとりながら、明確に区別されており、それぞれの集団の特性や違いをより精確に捉えることが確認できます。マハラノビス汎距離を導入することで、明らかにクラスタリングの精度と有用性が大きく向上することがわかります。<図3>
k-umeyamaの計算モデル
ランダムに一つずつ初期シードを選びそのシードと最短距離のdiを選び、すべてのデータポイントを計測。その平均距離をだした値をシグモイド関数で変換して、次シードを抽出するためのデータポイントのウエイト付けをします。その後、初回だけユークリッド距離で測り、サンプルをクラスターに所属させます。その後は、クラスター毎に平均と分散共分散、その一般逆行列を算出して、次にマハラノビス汎距離を測って所属クラスターの更新を繰り返します。クラスターの平均値が変化しなくなったら、終了です。<図4>

精度テスト(嘴の長さ、深さ等を用いたペンギンの分類)
クラスタリングの精度確認のため、パーマペンギンデータセットを用いて、ペンギンの成鳥の4種類のサイズから「ヒゲペンギン」、「ジェンツーペンギン」、「アデリーペンギン」の3群の正解のあるデータを、k-meansとk-means++、k-umeyamaでクラスター分析を行い比較しました。
k-umeyamaが、正解率0.982、k-means++は0.918、k-meansが0.775となり、k-umeyamaの分類精度が高い結果となりました。<図5>
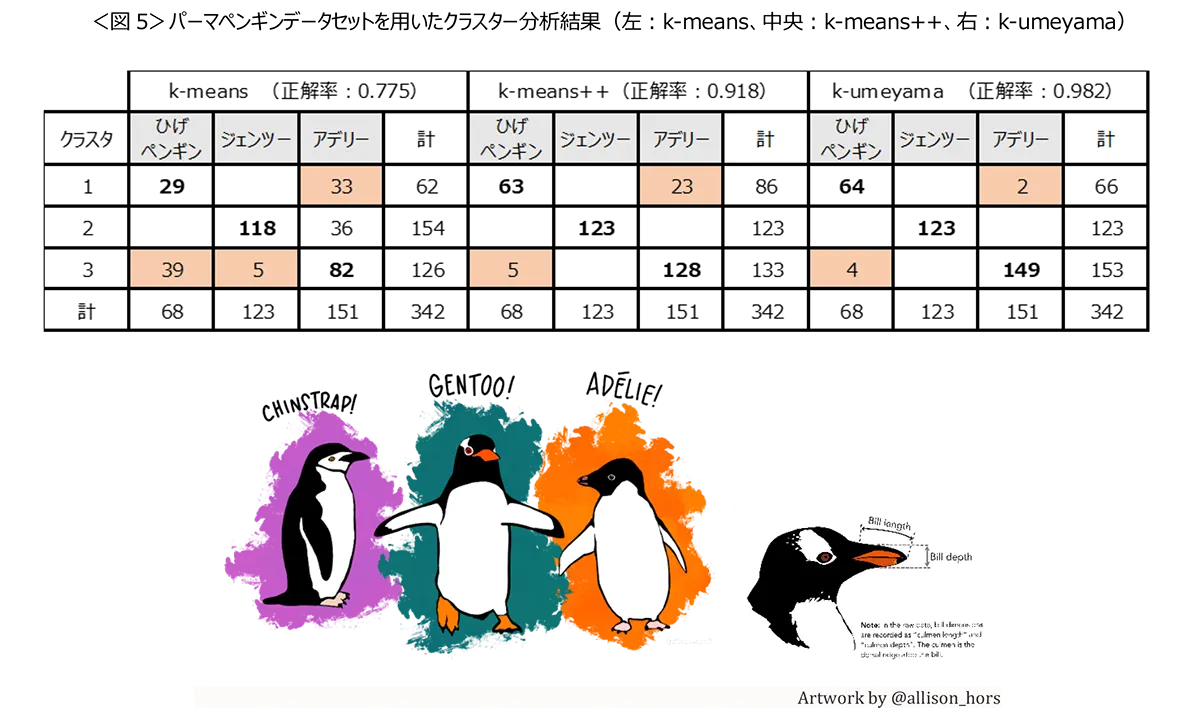
*パーマペンギンデータセットは、南極のパーマー基地周辺のパーマー群島の島々で観察されたアデリー、ヒゲペンギン、ジェンツーペンギンの成鳥のサイズ測定、嘴の長さ (mm)、 嘴の深さ (mm)、フリッパーの長さ (mm)、体重 (g)などのデータが含まれています。データはKristen Gorman博士とパーマー基地長期生態学研究(LTER)プログラムによって収集されたものを利用しています。
Horst, A. M., Hill, A. P., & Gorman, K. B. (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0. https://allisonhorst.github.io/palmerpenguins/. doi:10.5281/zenodo.3960218
【学会発表】
2023年8月29日(火)に行われた「日本行動計量学会 第51回大会」にて、k-umeyamaを発表いたしました。
【開発・研究協力】
朝野熙彦 元東京都立大学教授 「マハラノビス研究会」の研究代表者
【引用文献】
・朝野熙彦(2023)「マハラノビス研究会報告」日本マーケティング・リサーチ協会
・Arthur, D. and Vassilvitskii, S. (2007) k-means++: the advantages of careful seeding. SODA '07: Proceedings of the eighteenth annual ACM-SIAM symposium on discrete algorithms, 1027-1035.
・Cerioli, A. (2005) k-means cluster analysis and Mahalanobis metrics: A problematic match or an overlooked opportunity?. Statistica Applicata, 17(1), 61-73.
・水野欽司(1996)「多変量データ解析講義」朝倉書店
・Friedman H.P. & J. Rubin (1967) On Some Invariant Criteria for Grouping Data, Journal of the American Statistical Association, 62:320, 1159-1178
・Pillai, K. C. S. (1955). Some new test criteria in multivariate analysis. Annals of Mathematical Statistics, 26(1), 117-121.
・Hotelling, H. (1936). Relations between two sets of variates. Biometrika, 28(3/4), 321-377.
・Fisher,R.A. (1936) The use of multiple measurements in taxonomic problems. Annals of Eugenics, 7,179-188.
・Mahalanobis,P.C. (1936) On the generalized distance in statistics. Proceedings of the National Institute of Sciences of India, 2 (1), 49-55.
・Wilks, S.S. (1932). Certain generalizations in the analysis of variance. Biometrika,24, 471–494.
本レポートのダウンロードにより閲覧できる情報
本レポート(全18ページ)では、詳細情報をご覧いただけます。
≪引用・転載時のクレジット表記のお願い≫
本リリースの引用・転載時には、必ず当社クレジットを明記いただけますようお願い申し上げます。
<例>「マーケティング・リサーチ会社のクロス・マーケティングが開発した非階層クラスター分析k-umeyamaによると・・・」
詳細な調査データを無料にて配布しております
調査データは以下よりダウンロードできますので、ご確認ください。
既にアカウントをお持ちの方
新規登録(無料会員登録)の方
無料会員のサービス内容
- 市場調査レポートを無料でダウンロードいただけます。
- 会員限定のセミナーに無料でご参加いただけます。
- 分析ツール「Cross Finder2」を無料でご利用いただけます。
登録は無料。メールアドレス等の簡単な入力のみ。1分で完了します。
1.68 MB (自動取得)